What Happens to the Solubility of an Ionic Compound as Ionic Strength Increases to 0.5 M

Common Ion Effect

1. Last updated

2. Salvage as PDF

Page ID

1609

Learning Objectives

• Recognize common ions from diverse salts, acids, and bases.
• Summate concentrations involving mutual ions.
• Calculate ion concentrations involving chemic equilibrium.

The mutual-ion result is used to describe the effect on an equilibrium involving a substance that adds an ion that is a part of the equilibrium.

Introduction

The solubility products 1000 _sp'due south are equilibrium constants in hetergeneous equilibria (i.eastward., between 2 different phases). If several salts are present in a system, they all ionize in the solution. If the salts contain a common cation or anion, these salts contribute to the concentration of the mutual ion. Contributions from all salts must be included in the calculation of concentration of the common ion. For example, a solution containing sodium chloride and potassium chloride will have the following relationship:

\[\mathrm{[Na^+] + [K^+] = [Cl^-]} \label{1}\]

Consideration of charge balance or mass balance or both leads to the same conclusion.

Common Ions

When \(\ce{NaCl}\) and \(\ce{KCl}\) are dissolved in the aforementioned solution, the \(\mathrm{ {\colour{Green} Cl^-}}\) ions are common to both salts. In a system containing \(\ce{NaCl}\) and \(\ce{KCl}\), the \(\mathrm{ {\color{Green} Cl^-}}\) ions are common ions.

\(\mathrm{NaCl \rightleftharpoons Na^+ + {\colour{Green} Cl^-}}\)
\(\mathrm{KCl \rightleftharpoons K^+ + {\color{Light-green} Cl^-}}\)
\(\mathrm{CaCl_2 \rightleftharpoons Ca^{ii+} + {\color{Green} ii Cl^-}}\)
\(\mathrm{AlCl_3 \rightleftharpoons Al^{three+} + {\color{Green} 3 Cl^-}}\)
\(\mathrm{AgCl \rightleftharpoons Ag^+ + {\color{Green} Cl^-}}\)

For example, when \(\ce{AgCl}\) is dissolved into a solution already containing \(\ce{NaCl}\) (actually \(\ce{Na+}\) and \(\ce{Cl-}\) ions), the \(\ce{Cl-}\) ions come from the ionization of both \(\ce{AgCl}\) and \(\ce{NaCl}\). Thus, \(\ce{[Cl- ]}\) differs from \(\ce{[Ag+]}\). The post-obit examples show how the concentration of the common ion is calculated.

Example \(\PageIndex{one}\)

What are \(\ce{[Na+]}\), \(\ce{[Cl- ]}\), \(\ce{[Ca^2+]}\), and \(\ce{[H+]}\) in a solution containing 0.10 Grand each of \(\ce{NaCl}\), \(\ce{CaCl2}\), and \(\ce{HCl}\)?

Solution
Due to the conservation of ions, nosotros take

\(\mathrm{[Na^+] = [Ca^{two+}] = [H^+] = 0.10\: \ce Thou}\).

just

\(\begin{alignat}{iii}
&\ce{[Cl- ]} &&= && && \:\textrm{0.x (due to NaCl)}\\
& && && + &&\mathrm{\:0.20\: (due\: to\: CaCl_2)}\\
& && && + &&\mathrm{\:0.10\: (due\: to\: HCl)}\\
& &&= && &&\mathrm{\:0.40\: M}
\end{alignat}\)

Exercise \(\PageIndex{i}\)

John poured ten.0 mL of 0.10 Grand \(\ce{NaCl}\), 10.0 mL of 0.10 M \(\ce{KOH}\), and 5.0 mL of 0.20 K \(\ce{HCl}\) solutions together then he made the total volume to be 100.0 mL. What is \(\ce{[Cl- ]}\) in the final solution?

\(\mathrm{[Cl^-] = \dfrac{0.1\: M\times 10\: mL+0.2\: M\times five.0\: mL}{100.0\: mL} = 0.020\: M}\)

Le Châtelier's Principle states that if an equilibrium becomes unbalanced, the reaction volition shift to restore the balance. If a mutual ion is added to a weak acid or weak base of operations equilibrium, then the equilibrium will shift towards the reactants, in this case the weak acrid or base.

Instance \(\PageIndex{2}\)

Consider the lead(Two) ion concentration in this saturated solution of PbCl₂. The balanced reaction is

\[ PbCl_{2 (s)} \rightleftharpoons Pb^{ii+} _{(aq)} + 2Cl^-_{(aq)} \]

Defining \(south\) as the concentration of dissolved lead(Ii) chloride, then:

\[[Pb^{2+}] = s \]

\[[Cl^- ] = 2s\]

These values can be substituted into the solubility product expression, which can be solved for \(due south\):

\[\begin{eqnarray} K_{sp} &=& [Lead^{2+}] [Cl^-]^two \\ &=& south \times (2s)^ii \\ 1.7 \times 10^{-5} &=& 4s^3 \\ s^3 &=& \frac{1.7 \times x^{-5}}{4} \\ &=& 4.25 \times 10^{-half-dozen} \\ southward &=& \sqrt[3]{4.25 \times x^{-6}} \\ &=& i.62 \times 10^{-2}\ mol\ dm^{-3} \finish{eqnarray} \]​The concentration of atomic number 82(Ii) ions in the solution is 1.62 x 10^-ii M. Consider what happens if sodium chloride is added to this saturated solution. Sodium chloride shares an ion with lead(Ii) chloride. The chloride ion is common to both of them; this is the origin of the term "common ion effect".

Look at the original equilibrium expression again:

\[ PbCl_2 \; (southward) \rightleftharpoons Pb^{2+} \; (aq) + 2Cl^- \; (aq) \]

What happens to that equilibrium if extra chloride ions are added? According to Le Châtelier , the position of equilibrium will shift to counter the change, in this example, by removing the chloride ions by making extra solid lead(Ii) chloride.

Of course, the concentration of lead(II) ions in the solution is so small that only a tiny proportion of the extra chloride ions can be converted into solid lead(Two) chloride. The lead(II) chloride becomes fifty-fifty less soluble, and the concentration of pb(2) ions in the solution decreases. This blazon of response occurs with any sparingly soluble substance: it is less soluble in a solution which contains whatever ion which it has in common. This is the common ion effect.

A Simple Example

If an attempt is made to deliquesce some lead(II) chloride in some 0.100 M sodium chloride solution instead of in water, what is the equilibrium concentration of the pb(2) ions this time? As before, define s to be the concentration of the lead(II) ions.

\[[Pb^{2+}] = south \characterization{2}\]

The calculations are different from before. This time the concentration of the chloride ions is governed by the concentration of the sodium chloride solution. The number of ions coming from the atomic number 82(II) chloride is going to be tiny compared with the 0.100 K coming from the sodium chloride solution.

In calculations like this, it can be assumed that the concentration of the common ion is entirely due to the other solution. This simplifies the calculation.

So we assume:

\[[Cl^- ] = 0.100\; Chiliad \label{3}\]

The rest of the mathematics looks like this:

\brainstorm{equation} \begin{split} K_{sp}& = [Lead^{2+}][Cl^-]^2 \\ & = s \times (0.100)^2 \\ one.7 \times x^{-5} & = southward \times 0.00100 \finish{split} \end{equation}

therefore:

\brainstorm{equation} \brainstorm{split} s & = \dfrac{1.vii \times ten^{-five}}{0.0100} \\ & = 1.7 \times ten^{-3} \, \text{M} \end{split} \label{four} \end{equation}

Finally, compare that value with the simple saturated solution:

Original solution:

\[[Pb^{2+}] = 0.0162 \, M \characterization{5}\]

Solution in 0.100 Thou NaCl solution:

\[ [Atomic number 82^{2+}] = 0.0017 \, M \characterization{half dozen}\]

The concentration of the pb(Two) ions has decreased by a factor of about 10. If more concentrated solutions of sodium chloride are used, the solubility decreases farther.

Adding a common ion to a system at equilibrium affects the equilibrium composition, merely not the ionization constant.

Mutual Ion Effect with Weak Acids and Bases

Adding a mutual ion prevents the weak acid or weak base of operations from ionizing as much as it would without the added common ion. The common ion outcome suppresses the ionization of a weak acid by adding more of an ion that is a product of this equilibrium.

Example \(\PageIndex{2}\)

The common ion effect of H₃O⁺ on the ionization of acetic acrid

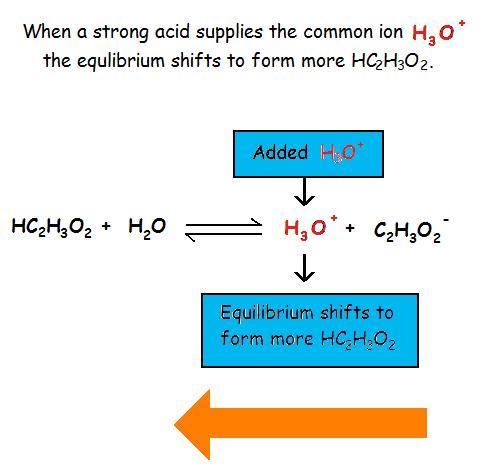
The common ion upshot suppresses the ionization of a weak base by adding more of an ion that is a product of this equilibrium.

Case \(\PageIndex{4}\)

Consider the common ion effect of OH^- on the ionization of ammonia

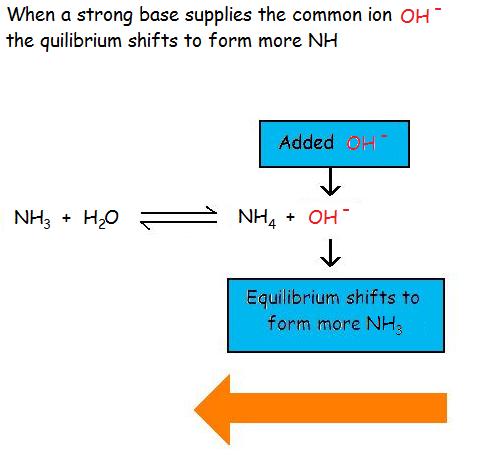
Calculation the common ion of hydroxide shifts the reaction towards the left to decrease the stress (in accordance with Le Cha telier's Principle), forming more reactants. This decreases the reaction quotient, because the reaction is being pushed towards the left to attain equilibrium. The equilibrium constant, Thou_b=one.viii*10^-5, does not change. The reaction is put out of balance, or equilibrium.

\[Q_a = \frac{[NH_4^+][OH^-]}{[NH_3]} \nonumber \]

At outset, when more hydroxide is added, the quotient is greater than the equilibrium constant. The reaction then shifts right, causing the denominator to increase, decreasing the reaction caliber and pulling towards equilibrium and causing \(Q\) to subtract towards \(Thou\).

Common Ion Consequence on Solubility

Adding a common ion decreases solubility, as the reaction shifts toward the left to save the stress of the excess product. Adding a mutual ion to a dissociation reaction causes the equilibrium to shift left, toward the reactants, causing precipitation.

Example \(\PageIndex{v}\)

Consider the reaction:

\[ PbCl_2(s) \rightleftharpoons Pb^{2+}(aq) + 2Cl^-(aq) \nonumber\]

What happens to the solubility of PbCl₂(s) when 0.1 Thou NaCl is added?

Solution

\[K_{sp}=1.7 \times x^{-v} \nonumber\]

\[Q_{sp}= i.8 \times 10^{-5} \nonumber\]

Identify the common ion: Cl^​-

Notice: Q_sp > Thousand_sp The add-on of NaCl has caused the reaction to shift out of equilibrium because there are more dissociated ions. Typically, solving for the molarities requires the assumption that the solubility of PbCl₂ is equivalent to the concentration of Pb^{2 +} produced because they are in a i:i ratio.

Because Yard_sp for the reaction is 1.seven×10^-5, the overall reaction would be (south)(2s)ⁱⁱ= ane.7×10^-5. Solving the equation for s gives due south= ane.62×ten^-ii M. The coefficient on Cl^- is ii, and then information technology is assumed that twice as much Cl^- is produced as Pb^{2 +}, hence the '2s.' The solubility equilibrium abiding tin can exist used to solve for the molarities of the ions at equilibrium.

The molarity of Cl^- added would be 0.ane M considering Na⁺ and Cl^- are in a one:ane ration in the ionic common salt, NaCl. Therefore, the overall molarity of Cl^- would be 2s + 0.1, with 2s referring to the contribution of the chloride ion from the dissociation of lead chloride.

\[\begin{eqnarray} Q_{sp} &=& [Atomic number 82^{2+}][Cl^-]^2 \\ 1.8 \times ten^{-v} &=& (s)(2s + 0.1)^2 \\ s &=& [Pb^{2+}] \\ &=& i.8 \times 10^{-3} One thousand \\ 2s &=& [Cl^-] \\ &\approx & 0.1 Yard \end{eqnarray} \]

Notice that the molarity of Lead^{two +} is lower when NaCl is added. The equilibrium constant remains the same because of the increased concentration of the chloride ion. To simplify the reaction, it can be causeless that [Cl^-] is approximately 0.1M since the formation of the chloride ion from the dissociation of pb chloride is so small. The reaction caliber for PbCl_ii is greater than the equilibrium abiding because of the added Cl^-. This therefore shift the reaction left towards equilibrium, causing atmospheric precipitation and lowering the current solubility of the reaction. Overall, the solubility of the reaction decreases with the added sodium chloride.

References

1. Harwood, William S., F. Thousand. Herring, Jeffry D. Madura, and Ralph H. Petrucci. General Chemistry Principles and Modernistic Applications. 9th ed. New Bailiwick of jersey: Prentice Hall, 2007.

Contributors and Attributions

• Emmellin Tung, Mahtab Danai (UCD)
• Jim Clark (ChemGuide)

• Chung (Peter) Chieh (Professor Emeritus, Chemical science @ Academy of Waterloo)

cowardhosturnelf1978.blogspot.com

Source: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Equilibria/Solubilty/Common_Ion_Effect

Share this post